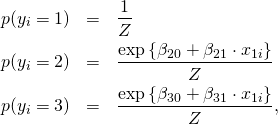The last post’s topic about multinomial logistic regression leads very nicely to a wide range of psychometric models for categorial responses, such as the Partial Credit Model (PCM) by Masters (1982). The PCM is a psychometric model that estimates the probability of a person’s response to an item based on characteristics of the item and the person’s latent ability. One particular nice feature of this model is the fact that Andrich’s rating scale model (RSM) and the dichotomous Rasch model (RM) are – as e.g. Mair and Hatzinger (2007) demonstrated – special cases of the PCM. It is fair to say that Samejima seems to have worked on a similar structure back in the sixties.

The focus of this post is on specifying the PCM as a graphical model, estimating the parameters via MCMC and crosschecking the results against the eRm package by Mair and Hatzinger (2007).

Let’s have a look at the formal structure of the PCM first. Starting point is the base distribution of multinomial logistic regression, sometimes called the “softmax activation function” in the machine learning literature:

(1)  

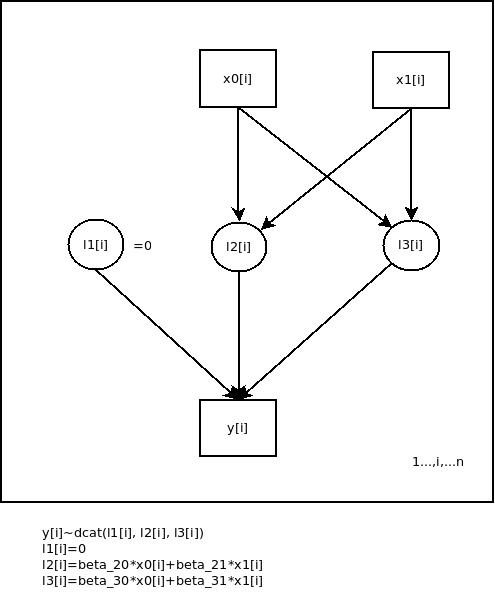
The next step is to linearily decompose the parameters with respect to the PCM. For simplicity I will consider the case of four categories per item only. Generalization to categories is simple and straight forward.

(2)  

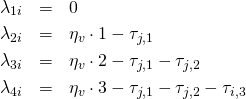
So, is the ability of person on the latent trait scale, and is the so called threshold parameter of item for the categories and . For example, a threshold parameter means that for item 1, given a latent ability of , the probability of choosing the category scored with 0 is equal to the probability of choosing the category scored with 1. This can be readily verified by for example plotting the item response functions for a set of threshold parameters. To estimate the PCM as a PGM, it is useful to introduce a multilevel perspective with respect to the persons’ abilities:

We assume that the latent abilities are normally distributed with a mean of zero and a variance of , which can be estimated from data. This is actually quite nice, because approaches exist to estimate the separability or reliability based on the variance of the latent trait distribution. Please note that the parametrization of the PCM above is a bit different from the original specification by Masters (1982).

The Bugs-Code for the model is straight forward:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# PCM.txt
model{
 
  for (i in 1:n)
  {
 
        lambda[1,i]<-0
        lambda[2,i]<-1*eta[id[i]]-tau[item[i],1]
        lambda[3,i]<-2*eta[id[i]]-tau[item[i],1]-tau[item[i],2]
        lambda[4,i]<-3*eta[id[i]]-tau[item[i],1]-tau[item[i],2]-tau[item[i],3]
 
        Z[i]<-exp(lambda[1,i])+exp(lambda[2,i])+exp(lambda[3,i])+exp(lambda[4,i])
 
        for(c in 1:4)
        {
        p[i,c]<-exp(lambda[c,i])/Z[i]
        }
        y[i]~dcat(p[i,1:4])
    }
 
 
 
# Priors
  for(j in 1:k)
  {
      tau[j,1]~dnorm(0,1.0E-6)
      tau[j,2]~dnorm(0,1.0E-6)
      tau[j,3]~dnorm(0,1.0E-6)  
  }
 
  for(i in 1:N)
  {
    eta[i]~dnorm(0,tau.eta)
  }
 
    tau.eta<-pow(sigma.eta,-2)
    sigma.eta~dunif(0,2)
}

Please note that the data have to be submitted in long format.

Now, let’s do something interesting with this. The following R-script uses the rsmdat example dataset in the eRm-package, transforms it into long format and submits it to JAGS. JAGS generates the posterior distributions the Bayesian way and returns the output to R. Subsequently, the threshold- and ability-parameters are estimated with the pcm()-function in the eRm-package and the results are compared graphically.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

# PCM.R
library(R2jags)
library(eRm)
 
# Load rsmdat
data<-rsmdat
# Number of thresholds per item
t<-max(data)
# Number of persons
N<-dim(data)[1]
# Number of items
k<-dim(data)[2]
# Transform data into long format
index=1
id<-c(0)
item<-c(0)
y<-c(0)
 
for(i in 1:N)
{
    for(j in 1:k)
    {
      y[index]=data[i,j]+1
      id[index]<-i
      item[index]<-j
      index<-index+1
    }
}
n<-length(y)
 
# Prepare arguments for jags()
data<-list("y","n","N","id", "item", "k")
parameters<-c("tau","eta", "sigma.eta")
inits <- function(){
list(tau = array(rnorm(t*k),c(k,t)), eta=rnorm(N), sigma.eta=runif(1)*2)
}
 
# Fit model
output<-jags(data, inits=inits, parameters, model.file="PCM.txt",
    n.chains=2, n.iter=4000, n.burnin=2000)
 
attach.jags(output)
 
# Checking against eRm ########
# Fit model with eRm
out<-PCM(rsmdat)
# Collect posterior means of threshold parameters 
# from jags output  
t1<-apply(tau[,1,],2,mean)
t2<-apply(tau[,2,],2,mean)
t3<-apply(tau[,3,],2,mean)
t4<-apply(tau[,4,],2,mean)
t5<-apply(tau[,5,],2,mean)
t6<-apply(tau[,6,],2,mean)
thresholds_pgm<-c(t1,t2,t3,t4,t5,t6)
# Collect threshold parameters from eRm
thresholds_eRm<-thresholds(out)$threshpar
# Plot PGM thresholds against eRm thresholds
plot(thresholds_eRm, ylim=c(-2,2.5), col=c("red"), ylab="tau")
points(thresholds_pgm, ylim=c(-2,2.5), col=c("green"))
 
# Collect posterior means of
# ability parameters from jags
eta_pgm<-apply(eta,2,mean)
# Collect ability parameters
# from eRm
eta_eRm<-person.parameter(out)$theta.table[,1]
plot(apply(rsmdat,1,mean),eta_eRm, xlim=c(0,3), col=c("red"), xlab="mean score",ylab="eta")
points(apply(rsmdat,1,mean),eta_pgm, xlim=c(0,3), col=c("green"))

I will spare you the outputs of JAGS and eRm but encourage you to download the scripts and to have a look yourself. Lets jump directly to the plots.

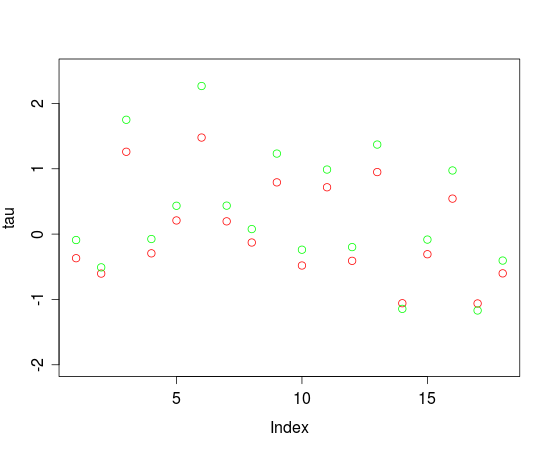
Fig. 1.: Threshold parameters estimated by eRm (red) and JAGS (green)

Visual inspection shows that eRm and JAGS essentially agree with regard to the locations of the threshold parameters. But there seems to be a difference between JAGS and eRm that is more pronounced for higher threshold parameters. The reason for this is probably the fact that JAGS samples from the posterior distributions of the parameters while eRm is using the CML-method for threshold estimation.

Let’s have a look at the ability estimates.

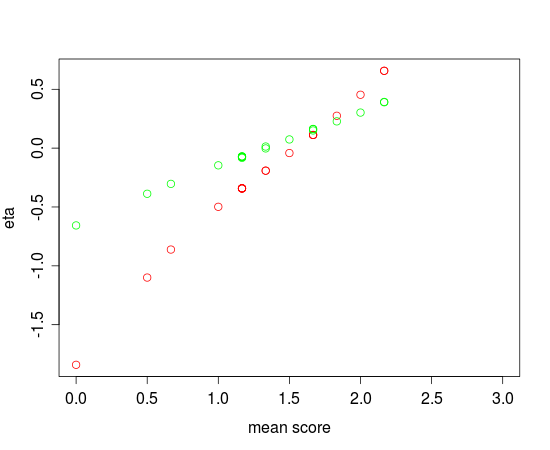
Fig. 2.: Ability estimates obtained by eRm (red) and JAGS (green) vs. mean score

In Figure 2, the differences between eRm and JAGS seem to be more pronounced. While the relationsship between the mean scores and the ability estimates seems to be more or less linear for the estimates produced by JAGS, this is not the case for eRm. The reason for this is probably the fact that the ability estimates generated by eRm were produced by using the ML-method with CML-estimates for the thresholds plugged in. Warm’s weighted ML method of person parameter estimation will most likely be included into future versions of eRm.

Which estimation method is better, Bayesian estimation with JAGS or CML combined with ML as implemented in eRm? It is hard to say from this comparison, a more systematic and thorough simulation study would be due that can be easily constructed from the code above. But note that MCMC-methods can be slow, especially for larger datasets.

The point of this post was mainly to demonstrate, how psychometric models could be fit to data with MCMC and to cross-check the results against eRm.

The scripts can be obtained here.

I decided to switch to English as I believe that this topic may be interesting for a wider audience. In the last post I have given a simple example of how the t-test for independent samples can be understood from a generalized linear modeling (GLM) perspective, how the model translates into a probabilistic graphcal model (PGM) and how to use Bayesian estimation techniques for parameter estimation. The main motivation behind that post was to show, how generalized linear models, probabilistic graphical models and bayesian estimation techniques can work together for solving statistical inference tasks, particularly in but not limited to Psychology.

I can hear the one or the other say: “Pah, t-test, peanuts!”. So in this post I would like to turn to something a bit more advanced: Multinomial Logit Regression (MLR). One task of MLR is to model the probability of a categorical response out of a set of mutually exclusive possible responses based on a set of predictors that may characterize for example the repondents. Typical questions are: Which characteristics of a person predict the choice of a specific party (Political Science) or a specific product (Economics) or a specific category on a multiple choice questionaire (Psychology). This type of model is also quite prominent in the machine learning community. One task is to classify text documents into mutually exclusive categories based on a set of text features as predictors.

Before we can specify the model as a PGM, we should have a look at its formal structure. First we need a probability distribution that is capable of modeling the probabilty of a certain categorical response based on a set of parametetrs. One such distribution is:

(1)  

This is quite neat. The denominator of that distribution is sometimes called the partition function or in German Zustandssumme from its use in statistical physics. It ensures that the probabilites for the possible events, states or responses sum up to one. Please note that the distribiution above has a little identification problem that can be solved by either setting to zero or by imposing a sum constraint over the parameters.

Here we set to zero:

(2)  

This also means that we are using category 1 as a reference category for inference. More on that later.

The trick in MLR is to simply decompose the parameters of the base distribution by simple linear regression equations:

(3)  

That’s basically it. The -weights have to be estimated from data, either by maximum likelihood or MCMC. To clarify the interpretation of the parameters and to elaborate a bit more, let’s assume we have three possible categories and only one predictor .

The probabilities of choosing a certain category are:

(4)  

with partiton function

Please note that runs over all three possible states of the system.

If we write down the log-probability-ratio (or log-risk-ratio) of choosing category 2 over category 1 we get:

(5)  

From this equation the meanings of the parameters become clear. is nothing but the log-probability-ratio of choosing category 2 over category 1, if is zero. is the expected change in terms of log-probabilty-ratios per unit increase of .

The log-probability-ratio of choosing category 3 over category 1 is:

(6)  

Here we are predicting log-probability-ratios of choosing category 3 over category 1 based on the predictor . is the log-probability-ratio of choosing category 3 over category 1, if is zero and is the expected change in terms of log-probability-ratios per unit increase of . Quite easy and very similar to multiple regression. The only thing one has to keep in mind is that we are predicting log-probability-ratios instead of changes in one continuous variable.

We are now in the position of having a graphical look at this simple model.

Fig. 1: Graphical representation of the simple multinomial logit regression model in the example

The variable y[i] is categorically distributed with parameters l1[i], l2[i] and l3[i]. l1[i] is set to zero for indentification purposes and l2[i] and l3[i] are linearily decomposed, e.g. due to the underlying design, if we are working experimentally. x0[i] is a dummy variable for the constants ( and ) of the regression equations and x1[i] is the predictor. The arrows symbolize dependencies between the nodes of the network.

To show how the model’s parameters of are estimated via MCMC in a Bayesian fashion, let’s introduce a little example. Let’s assume we have sampled individuals that are falling into two groups (). Each individual had the choice between 3 alternatives (). We are interested in the question: Do the groups differ with respect to the chosen alternatives? Or: Does the chosen category depend on group membership? If we crosstabulate the data in R we find:

1
2
3
4
5
6

> table(y,x)
   x
y    0  1
  1  5  3
  2 13  4
  3  2 14

By visual inspection we see that group 0 seems to have preference for alternative 2 and group 1 seems to have a preference for alternative 3. To model these data and to estimate the parameters via MCMC we have to translate the model into OpenBUGS code. This is straight forward from the graphical representation or the equations:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

#uo_multinom_reg.txt
model
{
  # Likelihood
  for(i in 1:n)
  {
 
    lambda[1,i]<-0
    lambda[2,i]<-beta_20+beta_21*x[i]
    lambda[3,i]<-beta_30+beta_31*x[i]
 
    # Partition function
    Z[i]<-exp(lambda[1,i])+exp(lambda[2,i])+exp(lambda[3,i])
 
    for(c in 1:3)
    {
      p[i,c]<-exp(lambda[c,i])/Z[i]
    }
    y[i]~dcat(p[i,1:3])
  }
 
  # Priors
  beta_20~dnorm(0,1.0E-6)
  beta_21~dnorm(0,1.0E-6)
  beta_30~dnorm(0,1.0E-6)
  beta_31~dnorm(0,1.0E-6)
}

The choice of normal priors for the parameters is motivated by the theoretical result that maximum likelihood etimates are asymptotically normally distributed. In addition, the precision of the priors is set to a very low value. So these distributions encode the prior information that we really do not know anything about the distributions of the parameters in the population yet and want to let the data speak for themselves as much as possible.

The R package R2OpenBUGS is used to control the OpenBUGS script:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# uo_multinom_reg.R
library(R2OpenBUGS)
data<-read.table("uo_multinom_reg.csv", sep=",", head=TRUE)
 
# data preparation
y<-data$wahl
x<-data$geschl
n<-length(y)
 
data<-list("y","x", "n")
 
parameters<-c("beta_20", "beta_30", "beta_21", "beta_31")
 
# Initial values for the markov chains
inits <- function(){
list(beta_20 = rnorm(1), beta_21=rnorm(1), beta_30=rnorm(1), beta_31=rnorm(1))
}
 
# Handing over to OpenBUGS
output<-bugs(data, inits=inits, parameters, model.file="uo_multinom_reg.txt",
    n.chains=2, n.iter=8000, n.burnin=1000)
 
# Printing the results
print(output, digits=2)

The output of OpenBUGS is

Inference for Bugs model at "uo_multinom_reg.txt", 
Current: 2 chains, each with 11000 iterations (first 1000 discarded)
Cumulative: n.sims = 20000 iterations saved
          mean   sd  2.5%   25%   50%   75% 97.5% Rhat n.eff
beta_20   1.01 0.55 -0.02  0.64  0.98  1.36  2.13    1  2200
beta_30  -1.09 0.94 -3.22 -1.67 -1.01 -0.44  0.49    1  2600
beta_21  -0.68 1.01 -2.66 -1.35 -0.69 -0.01  1.31    1  1400
beta_31   2.78 1.16  0.76  1.98  2.68  3.48  5.35    1  2100
deviance 74.84 3.01 71.11 72.61 74.17 76.25 82.69    1 20000

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule, pD = Dbar-Dhat)
pD = 4.1 and DIC = 79.0
DIC is an estimate of expected predictive error (lower deviance is better).

The statistics indicate that the markov process seems to have reached a stationary distribution.

The parameter beta_20 indicates a preference of category 2 over category 1 for group 0. But this difference is statistically not significant, probably due to small sample size. beta_30 indicates a preference of category 1 over category 3 for group 0, but from the percentiles of the posterior distributions we can see that this difference is also not significant statistically.

beta_21 is the contrast of group 1 to beta_20. As we can see, group 1 seems to have a slightly lower preference for category 2 over category 1 than group 0 in terms of log-probability-ratios, but this contrast is also not significant statistically.

beta_31 is statistically significant. Group 1 has a much stronger preference for category 3 over category 1 than group 0 in terms of log-probabilty-ratios.

Please note that this setup can be extended to include a larger set of continuous and categorical predictors. Also a multilevel extension of the model seems to be straight forward by “simply” including random effects into the linear regression equations.

The main objective of this post was to show in a simple way, how categorical data analysis techniques translate into a graphical representation that in terms can be used to estimate model parameters with MCMC-methods.

Grab the code here.

The proof of the pudding is in the eating. Von daher möchte ich an einem kleinen Beispiel zeigen, wie Generalisierte Lineare Modelle (GLMs), Probabilistische Graphische Modelle (PGMs) und Bayesianische Methoden praktisch zusammenspielen können. Was bietet sich besseres an, als der t-Test für unabhängige Stichproben? Um eine gewisse Vergleichbarkeit zu gewährleisten, beziehe ich mich auf das Beispiel zum t-Test in Bortz, Statistik, 6. Auflage (Tabelle 5.1., Seite 142). Zur praktischen Demonstration verwende ich die Software R und OpenBUGS. Die verwendeten Dateien finden sich hier.

Der t-Test für unabhängige Stichproben als GLM

Den meisten dürfte bekannt sein, dass die Fragestellung hinter dem t-Test sich auch mit der multiplen Regression, bzw. dem Allgemeinen Linearen Modell (ALM) bearbeiten lässt. Im Beispieldatensatz aus dem Bortz geht es darum zu prüfen, ob sich Männer und Frauen hinsichlich ihrer Belastbarkeit unterscheiden. Mit R geht das ganz einfach mit der Funktion glm().

1
2
3
4
5
6
7
8

# t-test_ua.R
 
# Laden der Daten
data<-read.table("B_5_1.csv", sep=",", head=T)
 
# Anpassung eines GLM mit Identitäts-Link-Funktion
m1<-glm(belast~geschl, data=data, family="gaussian")
summary(m1)

Es wird ein GLM mit Identitäts-Link-Funktion an die Daten angepasst. R liefert folgenden Output:

Call:
glm(formula = belast ~ geschl, family = "gaussian", data = data)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-18.242   -9.732   -2.221    9.289   25.800  

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  103.200      2.130  48.452   <2e-16 ***
geschlw        1.042      3.057   0.341    0.734    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

(Dispersion parameter for gaussian family taken to be 158.7827)

    Null deviance: 10498  on 67  degrees of freedom
Residual deviance: 10480  on 66  degrees of freedom
AIC: 541.54

Number of Fisher Scoring iterations: 2

Der mit Intercept bezeichnete Schätzer ist der vorhergesagte Mittelwert der Belastbarkeit der Männer und der Schätzer geschlw ist der Kontrast der Frauen zu dieser Baseline. Das bedeutet, dass Frauen einen um 1.042 Punkte höheren vorhergesagten Wert auf der Belastbarkeits-Skala aufweisen. Allerdings ist anhand des t-Werts von 0.341 deutlich ersichtlich, dass dieser Unterschied statistisch nicht signifikant ist. Dieses Ergebnis deckt sich im Wesentlichen mit dem Ergebnis im Bortz, wo ein t-Wert von -0.33 verzeichnet ist.

Der t-Test für unabhängige Stichproben als PGM

Das eben verwendete GLM lässt sich auch als grafisches Modell darstellen. Abbildung 1 zeigt die grafische Repräsentation.

Abbildung 1: Das GLM für den t-Test für unabhängige Stichproben als PGM

y[i] bezeichnet die Werte der abhängigen Variable und x1[i] und x2[i] bezeichnen die Werte der jeweiligen Prädiktoren in der Design-Matrix. mu[i] ist der lineare Prädiktor des Modells, der nach Maßgabe des zugrundeliegenden Designs linear zerlegt wird. sigma.y ist die Streuung der Residuen in der Population. Die Pfeile bezeichnen Abängigkeiten zwischen den Knoten des Netzwerks. Der Rahmen (plate notation) um die Knoten symbolisiert, dass Beobachtungen vorliegen. Formal lässt sich das Modell relativ einfach darstellen:

Es wird also angenommen, dass die beobachteten Werte einer Normalverteilung mit der Mittelwertsstruktur und der Varianz entstammen. Oder anders gesagt, es wird angenommen, dass die Residuen in der Population mit der Varianz normal verteilt sind. Wenn die Dummy-Codierung für der Spezifikation einer Konstanten entspricht, handelt es sich also um nichts anderes, als um eine einfache lineare Regression in grafischer Darstellung.

Bayesianische Bestimmung der Parameter

Die Parameter , und die Varianz müssen aus den Daten geschätzt werden. Wie dies auf Bayesianische Art mit Hilfe der MCMC-Methode, R und OpenBUGS geschehen kann, sei kurz gezeigt. Zunächst muss eine Datei mit der Modellspezifikation für OpenBUGS erstellt und gespeichert werden.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# t-test_ua.txt
model
{
  # Likelihood
  for (i in 1:n)
  {
  y[i] ~ dnorm (mu[i], tau.y)
  mu[i]<-beta0*X[i,1]+beta1*X[i,2]
  }
  # Prior-Distributions
  beta0 ~ dnorm(0, 1.0E-6)
  beta1 ~ dnorm(0, 1.0E-6)
  tau.y <- pow(sigma.y, -2)
  sigma.y ~ dunif (0, 1000)
  # Cohen's delta
  delta<-(beta1)/sigma.y
}

Die Spezifikation des Modells erfolgt im Abschnitt #Likelihood. Anschließend werden die Prior-Verteilungen spezifiziert, die hier relativ uninformativ gehalten sind. Als besonderer Bonus wird die Posterior-Verteilung von Cohen's delta auf Basis des MCMC-Prozesses erzeugt.

OpenBUGS wird durch das R-Skript angesteuert, das auch die Daten an OpenBUGS übergibt.

9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

 
library(R2OpenBUGS)
# Vorbereitung der Daten zur 
# Übergabe an OpenBUGS
y<-data$belast
X<-model.matrix(m1)
n<-length(y)
data<-list("y","X", "n")
 
# Spezifikation der zu bestimmenden Parameter
parameters<-c("beta0", "beta1", "sigma.y", "delta")
 
# Übergabe an OpenBUGS
output<-bugs(data, inits=NULL, parameters, model.file="t-test_ua.txt",
    n.chains=2, n.iter=5000, n.burnin=1000)
 
# Ausgabe der Ergebnisse
print(output, digits=2)
 
# Histogramm von beta1
hist(beta1,100)
# Histogramm von Cohen's delta
hist(delta,100)

Um die Konvergenz des Markov-Prozesses zu überprüfen, kommen zwei Markov-Ketten zum Einsatz. Der Prozess durchläuft 5000 Iterationen, wobei die Burn-In-Phase 1000 Iterationen beträgt. Die Startwerte des Markov-Prozesses werden im Beispiel zufällig erzeugt.

OpenBUGS liefert folgenden Output:

Inference for Bugs model at "t-test_ua.txt", 
Current: 2 chains, each with 5000 iterations (first 1000 discarded)
Cumulative: n.sims = 8000 iterations saved
              mean   sd   2.5%    25%    50%    75%  97.5% Rhat n.eff
beta0       103.25 2.14  99.06 101.80 103.20 104.70 107.40    1  8000
beta1         0.99 3.07  -5.06  -1.02   0.97   2.98   7.06    1  8000
sigma.y      12.84 1.15  10.82  12.03  12.75  13.55  15.35    1  8000
delta         0.08 0.24  -0.39  -0.08   0.08   0.23   0.55    1  8000
deviance    538.62 2.55 535.80 536.80 538.00 539.70 545.00    1  4300

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule, pD = Dbar-Dhat)
pD = 2.9 and DIC = 541.5
DIC is an estimate of expected predictive error (lower deviance is better).

Von Interesse sind hier besonders die Mittelwerte und Perzentile der Posterior-Verteilungen und Rhat. Der Schätzer für die mittlere Belastbarkeit der Männer beträgt 103.25 und der geschätzte Kontrast der Frauen zum Mittelwert der Männer beträgt 0.99. Das 95%-Kredibilitäts-Intervall für liegt zwischen -5.06 und 7.06. Damit ist der Unterschied zwischen Männern und Frauen statistisch nicht signifikant. Der Schätzer für Cohen's delta beträgt 0.08. Dieses Ergebnis ist mit dem Resultat im Bortz kongruent. Zudem wurde das 95%-Kredibilitäts-Intervall für Cohen's delta ermittelt. Dieses Intervall liegt zwischen -0.39 und 0.55, was ebenfalls darauf hindeutet, dass der Unterschied zwischen Männern und Frauen hinsichtlich der Belastbarkeit statistisch nicht signifikant ist. Die Statistik Rhat zeigt an, dass die zwei eingesetzten Markov-Ketten gegen die Posterior-Verteilung der Parameter konvergieren.

Was auffällt ist, dass in der Ausgabe keine p-Werte vorkommen. Das ist nicht weiter tragisch, da die Inferenz auf Basis der Kredibilitäts-Intervalle geschieht. Wer aber dennoch nicht auf p-Werte verzichten möchte, kann diese einfach aus den Posterior-Verteilungen berechnen. Zum Abschluss sei hier noch das Histogramm der Posterior-Verteilung von Cohen's delta dargestellt.

Abbildung 2: Posterior-Verteilung von Cohen's delta

Das war zugegebener Maßen ziemlich viel Information auf einmal und Anspruch dieser Blog-Post kann es nicht sein, die Hintergründe der hier verwendeten Verfahren umfassend zu erklären. Den interessierten Leser oder die interessierte Leserin verweise ich auf die Literatur. Mir war es jedoch wichtig, einmal an einem einfachen Beispiel zu zeigen, wie GLMs, PGMs und Bayesianische Methoden ineinandergreifen können.

Als Übung empfehle ich zu überlegen, wie das grafische Modell und der OpenBUGS-Code im Falle der multiplen Regression aussehen müssten. Bonuspunkte gibt es für die Erzeugung der Posterior-Verteilung für den Determinations-Koeffizienten, bzw. . Interessant wäre auch ein systematischer Vergleich der hier dargestellten Methode zur Erzeugung von Kredibilitäts-Intervallen für Effektstärke-Indices mit der „frequentistischen" Methode zur Erzeugung von Konfidenz-Intervallen auf Basis von nichtzentralen Verteilungen.

In der methodischen Welt ist einges in Bewegung, das zum Teil noch wenig Eingang in die Anwendung im deutschsprachigen Raum genommen hat. Ein Ziel dieses Weblogs ist es, methodisch interessierten Anwendern einen praktischen Einstiegspunkt in die neueren oder hierzulande weniger verbreiteten Verfahren zu bieten und darüber zu informieren, was mich methodisch interessiert. Darüber hinaus wird es auch das eine oder andere Fotografische zu sehen und zu lesen geben.

Methodisches

Methodisch interessieren mich zur Zeit vor allem für drei Punkte: 1. Generalisierte Lineare (Gemischte) Modelle, 2. Bayesianische Methoden, 3. Probabilistische Graphische Modelle.

1. Generalisierte Lineare (Gemischte) Modelle (GLMMs)

GLMMs sind eine relativ weitreichende Modellklasse, die sich zur Bearbeitung einer Fülle von Forschungsfragestellungen eignet und  meines Erachtens in der Psychologie im deutschsprachigen Raum noch relativ wenig rezipiert ist. Eine Menge gängiger klassischer Verfahren lassen sich im Rahmen der GLMMs darstellen. Diese sind z.B. das Allgemeine Lineare Modell (ALM), die logistische Regression zur Analyse von dichotomen und kategorialen Daten, die Poisson-Regression zur Analyse von Häufigkeiten sowie die Mehrebenen-Extensionen dieser Verfahren. Auch gängige Item-Response-Modelle der Psychometrie, wie das dichotome Rasch-Modell oder das Partial-Credit-Modell, sind als GLMMs verstehbar.

Warum GLMMs?

In der psychologischen Methodenausbildung lernt man gewissermaßen “bottom-up”. Es werden Einzelverfahren, wie. z.B. die t-Tests und die Varianzanalysen gelernt, die zunächst scheinbar unverbunden nebeneinander stehen und erst gegen Ende der Ausbildung werden die größeren Zusammenhänge mit der Einführung des ALM im Rahmen der Multivariaten Verfahren sichtbar. Meiner Ansicht nach ist ein alternativer Ansatz, direkt mit dem ALM als Spezialfall von GLMMs einzusteigen, dieses um die Mehrebenen-Analyse zu erweitern und dann zur (gemischten) logistischen Regression und der (gemischten) Poisson-Regression zur Häufigkeitsanalyse voranzuschreiten. Der Vorteil dieser Vorgehensweise liegt vermutlich darin, dass GLMMs formal ein relativ kompaktes, koheräntes und zusammenhängendes System darstellen, das in der globalen statistischen Gemeinschaft gut rezipiert ist. Wer die multiple Regression und die Mehrebenen-Analyse versteht, sollte keine größeren Schwierigkeiten mit den Erweiterungen haben. Sind die Grundlagen verstanden, ist der Kopf frei dafür, den Hauptfokus auf die Planungsphase einer Untersuchung zu legen und zu klären, wie eine konkrete Modellspezifikation auszusehen hat, um eigene Forschungsfragestellungen zu bearbeiten. Wenig bekannt scheint es auch zu sein, dass sich GLMMs, bzw. Multilevel-Analysen auch dazu eignen, Experimentaldaten zu analysieren oder psychometrische Messmodelle zu erzeugen.

Die relative Novität dieser Verfahren bringt es mit sich, dass hier noch einiges zu tun ist, auch Lehrbücher, speziell für Psychologen oder Human- und Sozialwissenschaftler sind rar.

2. Bayesianische Methoden

Unter anderem im Rahmen der Kontroversen um den klassischen Signifikanz-Test nach Fisher habe ich begonnen mich mit Bayesianischen Methoden auseinanderzusetzen. Die Bayesianische Statistik unterscheidet sich in einigen wesentlichen Punkten vom “klassisch-frequentistischen” Ansatz. Zu nennen  wären z.B. fundamentale Unterschiede im Wahrscheinlichkeitsbegriff und die Verwendung von Prior-Verteilungen. Dazu, welcher Ansatz nun “der Richtige” ist, möchte ich mich hier nicht äußern. Das Feld ist historisch durch zahlreiche Debatten geprägt und meines Erachtens macht es erst dann Sinn sich mit dem Bayesianischen Ansatz auseinanderzusetzen, wenn die klassischen Ansätze von Fisher und Neyman-Pearson verstanden worden sind. Nichtsdestotrotz zeigen sich auf dem Lehrbuch-Markt im anglo-amerikanischen Raum einige Entwicklungen, die in Richtung Bayes weisen.

Warum Bayesianische Methoden?

Persönlich sehe ich im Bayesianischen Ansatz einige Vorteile gegenüber den klassischen Ansätzen:

• Die Verwendung von MCMC-Methoden ermöglicht es, sog. Posterior-Verteilungen von Parametern auf der Basis von Daten, einer Modell-Likelihood und von Prior-Verteilungen zu erzeugen, was potentiell von der Abhängigkeit von tabellierten Verteilungen befreit. Die Posterior-Verteilungen lassen sich für Inferenz-Zwecke nutzen. Um ein Beispiel zu geben: Die Freiheitsgrade der t-Statistiken bei der Multilevel-Analyse sind nach Douglas Bates streng genommen unbekannt. Eine potentielle Lösung für das Problem besteht darin, die Posterior-Verteilungen der entsprechenden Parameter auf Basis der MCMC-Methode zu erzeugen und die Signifikanz auf der Basis sog. Kredibilitäts-Intervalle zu evaluieren.
• Theoretisch lassen sich Posterior-Verteilungen von abgeleiteten Statistiken, wie z.B. von Reliabilitäts-Indices oder Effektstärke-Indices generieren. Anstatt nur einen Punktschätzer zu verwenden, fallen Kredibilitäts-Intervalle dieser Indices an, die sich zum Zweck der Inferenz nutzen lassen.
• Das Problem von fehlenden Werten ist bei der Verwendung von MCMC-Methoden vermutlich kein Problem. Anstatt Techniken der Multiplen-Imputation zu verwenden, fallen ohne besondere Vorkehrungen modellbasiert Kredibilitäts-Intervalle für die Lage der fehlenden Werte auf Basis der vorhandenen Informationen an. Diese vorhanden Informationen sind die Daten, ein statistisches Modell und die entsprechenden Prior-Verteilungen.
• Die Modellgüte lässt sich über sog. Posterior-Prediktive-Checks evaluieren. Hier wird die Lage von empirisch beobachteten, abgeleiteten Statistiken mit der unter einem Modell angenommenen Verteilung der Lage verglichen, um zu überprüfen, wie gut das Modell die beobachteten Daten abbildet, ähnlich, wie dies auch beim parametrischen Bootstrapping der Fall ist.

Bayesianische Methoden stellen ein relativ breites Feld der Forschung dar, das bis jetzt in der Psychologie noch wenig oder gar nicht genutzt wird.

Bei all den vermuteten Vorteilen stellt sich zu Recht die Frage, was eigentlich die Nachteile der Verwendung dieser Methoden sein könnten.

• Die Mathematik und die Anwendung ist bisweilen relativ komplex
• Der Bayesianische Wahrscheinlichkeitsbegriff unterliegt einer Kontroverse
• Die Verwendung von Prior-Verteilungen unterliegt historisch ebenfalls einer Kontroverse, da hierüber Vorinformationen des Anwenders in die Analyse mit einfließen können. Irgendwo las ich: „Dies ist ein Vorteil oder Nachteil, je nachdem, wen man fragt.” In der Praxis scheint sich eingebürgert zu haben, möglichst uninformative Prior-Verteilungen zu verwenden, um Subjektivität zu minimieren. Ferner ist der Bayes Ansatz mit dem klassischen Maximum-Likelihood-Ansatz kompatibel, sofern uninformative Prior-Verteilungen verwendet werden.

Insgesamt kann gesagt werden, dass in diesem Feld eine Menge in Bewegung ist, was sich z.B. auch darin zeigt, dass Bayesianische Schätzverfahren in die bekannte Analysesoftware MPlus Eingang gefunden haben. Aus der Perspektive einer psychologischen Methodenforschung ist hier noch eine Menge zu tun.

3. Probabilistische Graphische Modelle

Durch meine Auseinandersetzung mit Bayesianischen Verfahren bin ich letztlich auf Probabilistische Graphische Modelle (PGMs) gestoßen, die sich u.a. in der machine learning community einer gewissen Beliebtheit zu erfreuen scheinen. PGMs entspringen einer Fusion von Wahrscheinlichkeitstheorie und der mathematischen Graphentheorie. Der für mich relevante Aspekt dieser Modelle liegt darin, dass sich eine Vielzahl in der Psychologie verwendeten Modelle, insbesondere Modelle mit latenten Variablen, als PGM darstellen lassen. Der graphische Ansatz erleichtert meines Erachtens das Nachdenken über Unabhängigkeitsbeziehungen zwischen Variaben und das Verständnis von komplexen Modellen. Unter dieser Persepektive sind die bekannten linearen Strukturgleichungsmodelle in der Tat auch PGMs. Zudem bedienen sich viele Programme zur Anwendung der MCMC-Methode, wie z.B. JAGs oder OpenBUGS des graphischen Ansatzes zur Modellspezifikation. In diesen Bereichen bin ich derzeit selbst bei der Exploration.

Zusammenfassend kann gesagt werden, dass es aus meiner Sicht im methodischen Bereich einiges zu tun gibt:

1. Vermittelung von GLMMs unter dem besonderen Aspekt der Anwendung auf (psychologische) Forschungsfragestellungen
2. Nähere Untersuchung der Eignung des Bayesianischen Ansatzes für die psychologische Forschung
3. Exploration der Modellklasse der PGMs unter dem besonderen Aspekt der Verbindung zu schon bekannten Modellen in der Psychologie und auch als Möglichkeit der Modellgenerierung

Fotografisches

Privat interessiere ich mich für Fotografie in ihren kulturellen, historischen und praktischen Aspekten. Heutzutage ist es schwierig, berufliches und privates zu trennen. Von daher werde ich der Einfachheit halber – und damit das Ganze nicht zu methodenlastig wird – dieses Weblog auch dazu nutzen, ein paar Dinge zum Thema Fotografie aus meiner Perspektive zu schreiben. Vermutlich wird es auch das eine oder andere Bild zu sehen geben. Ein tolles Buch zum Einstieg in die Thematik „Fotografie” ist z.B. Michel Frizot (Hrsg.) (1998). Neue Geschichte der Fotografie. Köln: Köhnemann.